Home
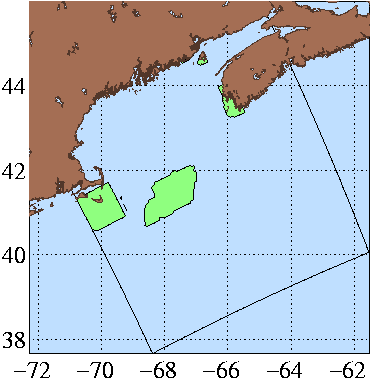
Dynamically Adjusting Feature Model Fields
Tidal mixing locations
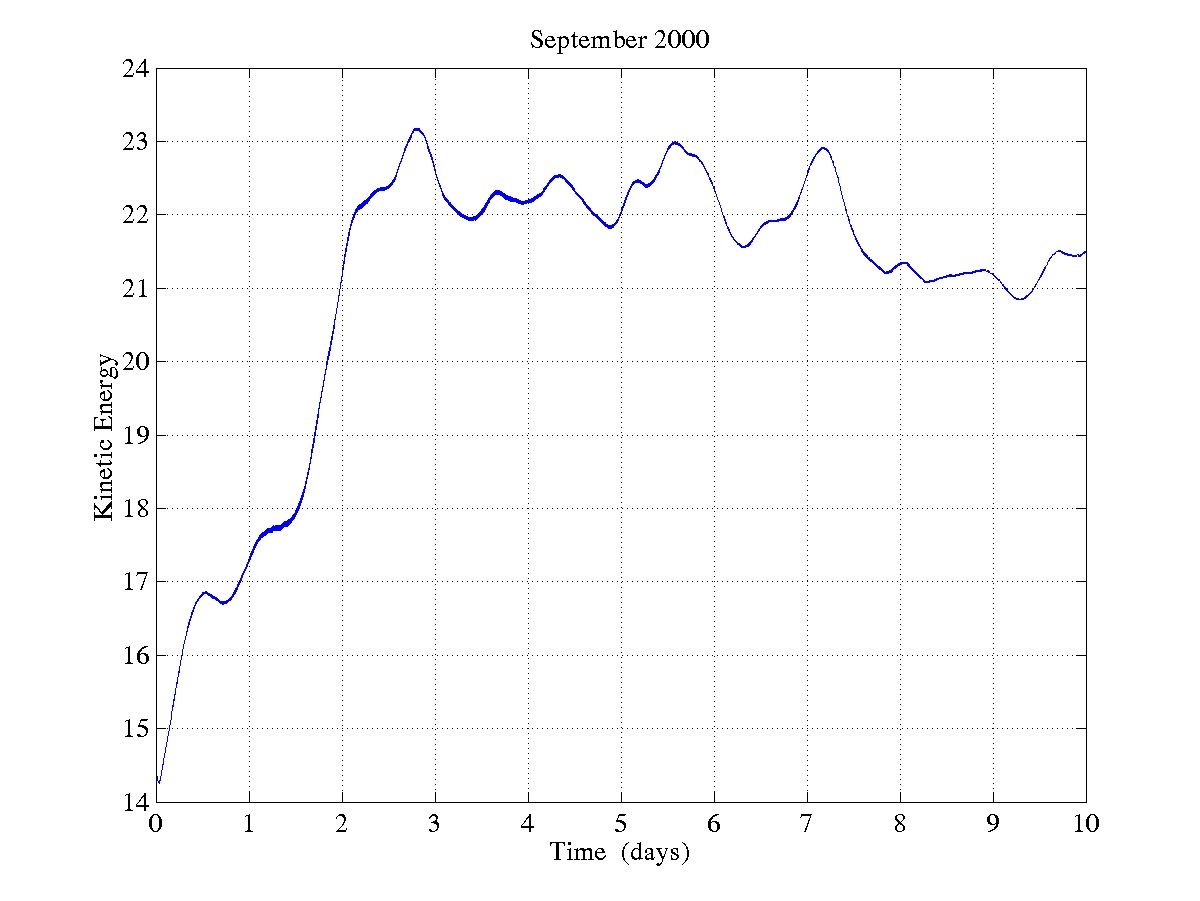
September 2000
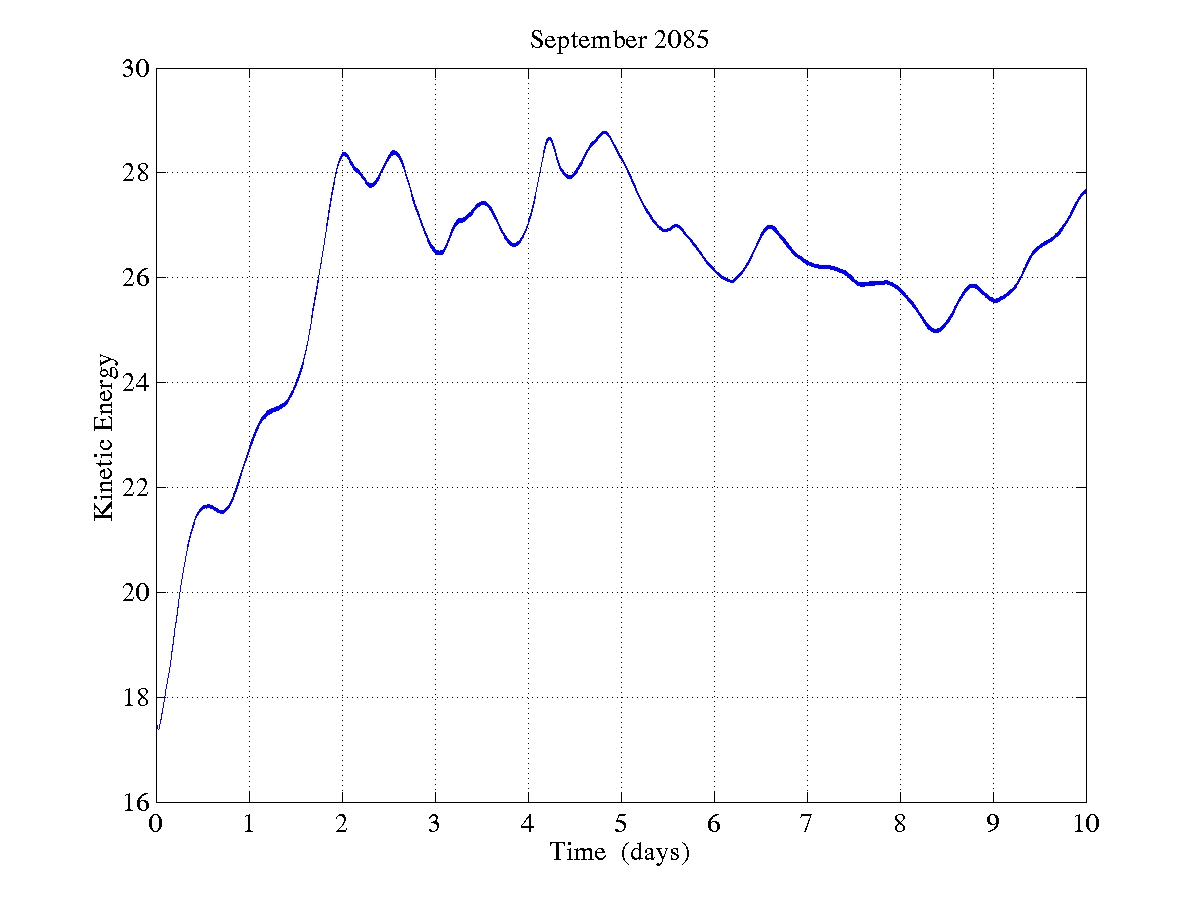
September 2085

The feature model initialization fields are dynamically adjusted using the HOPS PE model. One category of features that needs to be explicitly dealt with is the tidal fronts. Loder & Greenberg (1986) highlighted a number of tidal fronts associated with specific locations. To expedite our work, we chose the simplest parameterization of these tidal fronts by specifying regions of enhanced tidal mixing. We implement this by specifying 4 i-j boxes in the modeling domain. Within each box we specify a minimum active depth. At each point in a box where the model bottom topography is < the minumum active depth, the vertical mixing coefficients in the water column are required to be at least a set minimum value (in this exercise 50 cm2/s). The resulting locations of enhanced mixing are shown in the figure to the right.

Both the 2000 and the 2085 simulations are run for 10 days to adjust the geostrophic initialization to primitive equation dynamics. The volume averaged kinetic energy shows that, on average, the models equilibrate in roughly 2-3 days. However, there is still velocity adjustment at the shelf/slope front by Georges Bank even after 10 days.

Both simulations are structurally very similar. This shouldn't be surprising as they both start with the same features, differing only by horizontally constant shifts of T/S. The most readily visible difference is the warming of the shelf waters. The greater warming on the shelf erodes some of the temperature signal of the shelf/slope front.

The overall similarity between the 2000 and 2085 fields suggests several paths for future work to allow for more effects of climate change:

  1. Use the relevant atmospheric forcing for both 2000 and 2085 simulations. This could be done either during or after the initial dynamic adjustment.
  2. Instead of constant shifts, use the objective analysis to create large scale shift fields for the shelf and slope waters.
  3. Parameterizing river input relevant for both 2000 and 2085.
  4. Use tidal forcing relevant for both 2000 and 2085.

Additionally, given the overall uncertainties in this work, an ensemble approach to generate statistics as well as a central estimate would be encouraged.

Simulation Details

Both simulations were made with a 225 second time step. The lateral open boundaries were forced with a variant of the Perkins et al. (1997) nested boundary condition, which allows radiation of small scales in a nested model. In our cast the "larger nesting model" was replace by persisted initial boundary values, which helped to maintain the Maine Coastal Current inflow. The horizontal sub-gridscale was parameterized by a Shapiro filter (Shapiro, 1970). In particular a fourth order filter was used for tracers and velocity, a (weaker) eighth order filter was used for the surface pressure. In the vertical, the sub-gridscale was parameterized by a second order diffusion term where the coefficients are function of the Richardson number, following the Pacanowski and Philander (1981) scheme. The peak viscosity/diffusivity was set to 50 cm2/s, the background viscosity was set to 0.5 cm2/s, and the background diffusivity was set to 0.05 cm2/s. Near the surface (5m), the vertical viscosity and diffusivity coefficients are bounded below by values (15 cm2/s for viscosity and 0.75 cm2/s for diffusivity) to parameterize wind mixing. At depths where the water column is gravitationally unstable, the vertical viscosity/diffusivity were bounded below by 50 cm2/s. Finally, a Rayleigh friction parameterization of drag induced by the bottom (Lermusiaux, 1997) was used. The temporal decay scale was 3600s and the spatial decay was 1.5 (model levels from the bottom).

Lermusiaux, P.F.J. (1997) Error Subspace Data Assimilation Methods for Ocean Field Estimation: Theory, Validation and Applications. PhD Thesis, Harvard University, Cambridge, MA.

Loder, J. W. and D. A. Greenberg, (1986) Predicted positions of tidal fronts in the Gulf of Maine. Cont. Shelf Res., 6(3), 397-414.

Pacanowski, R.C. and G.H. Philander (1981) Parameterization of Vertical Mixing in Numerical Models of Tropical Ocean. J. Phys. Oceanogr., 11, 1443-1451.

Perkins, A.L., L.F. Smedstad, D.W. Blake, G.W. Heburn, & A.J. Wallcraft (1997) A new nested boundary condition for a primitive equation ocean model. J. Geophys. Res., 102(C2). 3483-3500.

Shapiro, R. (1970) Smoothing, Filtering and Boundary Effects. Reviews of Geophysics and Space Physics, 8(2), 359-387.