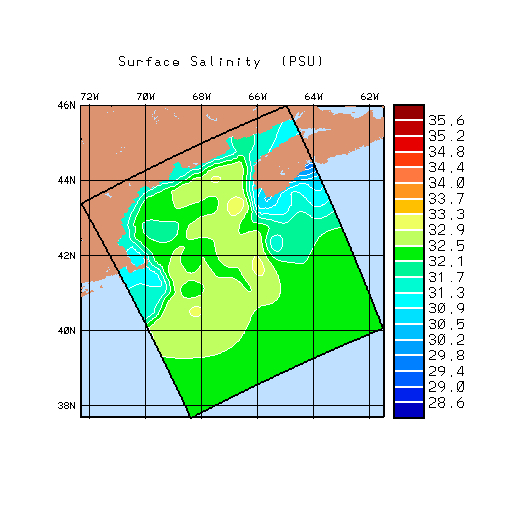
Shelf Climo OA + MCC

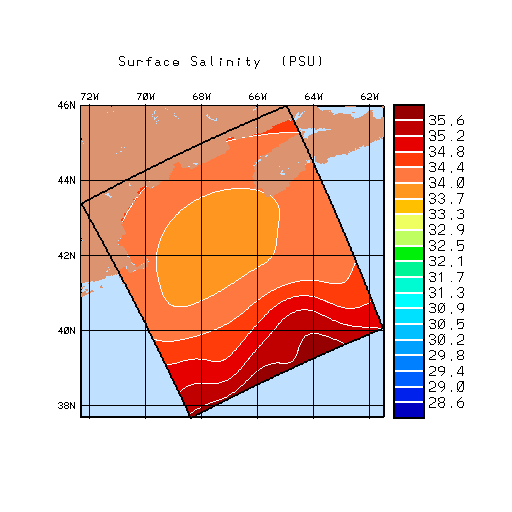
Slope GDEM OA

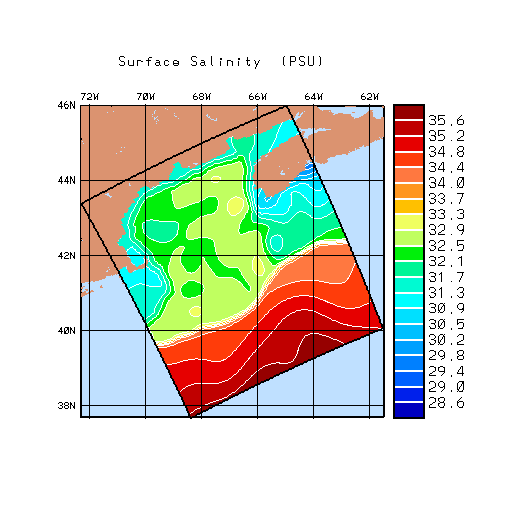
Shelf/Slope FM

The shelf/slope front is the separator between cool, fresh water flowing southward along the shelf from the Labrador Sea and the warm saline water flowing northward along the continental slope. From Georges Bank south, the front is, on average attached at the foot to the 100m isobath and slopes outward with an average slope of 0.002 and observed slopes between 0.001 and 0.008. Off the Scotian shelf, the shelf water typically overruns the slope water resulting in a detached foot.

To model this separator, we create separate realizations of the domain using only shelf or slope data. We then meld these estimates with a hyperbolic tangent function

where

(s,η) are the along and across front coordinates

z is the depth

θ(s) is the frontal slope (a function of the along-front coordinate)

w is the width of the front

The frontal location is defined as the location of the center of the front at the oceans surface, typically obtained from satellite SST. To specify the variable frontal slope we define a frontal "foot" (i.e. a curve where we expect the front to be located at a depth of 100m). The frontal slope, at each point s_i of the frontal location curve, is simply the minimum distance (m) between s_i and the frontal "foot" divided into 100m, subject to 0.001 < θ(s) < 0.008. We constructed our default frontal foot from a 30 arcsecond topography as

1. The 100m isobath is simplified by cutting across the mouths of the Gulf of Maine, the Gulf of the Saint Lawrence and a canyon or inlet north of the Gulf of the Saint Lawrence. Also removed is a shoal off Nova Scotia
2. The 300m isobath is simplified by cutting across the mouths the Gulf of the Saint Lawrence and a canyon or inlet north of the Gulf of the Saint Lawrence.
3. Each of these simplified contours is sub-sampled by a factor of 27 using a median sub-sampling. This subsampling is done to keep small scale topography features out of the default curve.
4. The simplified 100m isobath south of the eastern extremum of Georges Bank is joined to the simplified 300m isobath to the North.

In order to model the Scotial shelf over-shoot (and limit the arbitrary placement of slope waters in the deep portions of the Gulf of Maine) we also define a deep divider curve for melding between the depths 100m and 300m. (Below 300m there is no Gulf of Maine and we just use the slope waters). This deep divider curve is also defined from a 30 arcsecond topography:

1. A contour 5km shoreward of simplified 100m isobath is constructed.
2. The contour is sub-sampled by a factor of 27 using a median sub-sampling.

For this problem we have no satellite SST to define the surface frontal location. We use a default frontal location constructed from the default frontal foot to yield a slope of 0.002:

1. A contour 50km offshore of the default shelf/slope foot is constructed.
2. The contour is sub-sampled by a factor of 27 using a median sub-sampling.

Once the temperature and salinity fields have been melded, the resultant density field is integrated with a 2000m level of no motion to obtain a geostrophic streamfunction. This first guess streamfunction, ψ₁, is then fed into the Poisson equation

subject to the kinematic constraint that ψ is constant along coastlines. This constraint against flow into the solid boundaries improves the definition of the MCC in the feature model fields.