Multiscale Data Assimilation
|
P.F.J. Lermusiaux, P.J. Haley, Jr., J. Lin Massachusetts Institute of Technology
|
Project Summary Ongoing MIT-MSEAS Research Background Information Specific Research Tasks References
|
|
|
| This research is sponsored by the Office of Naval Research. | |||
Project Summary
Ocean modeling is the process of developing and utilizing theoretical and computational models for the understanding and prediction of ocean dynamics. Data assimilation is the process of quantitatively estimating dynamically evolving fields by combining information from observations with those predicted by models, ideally respecting nonlinear dynamics and capturing non-Gaussian features, without heuristics or ad hoc approximations. Even though ocean dynamics often involve multiple scales, the theory for rigorous multiscale data assimilation is still in its infancy.
Background information is available below.
| Top of page |
Ongoing MIT-MSEAS Research
Long-Term Goals:
The present project is to research next-generation multiscale data assimilation, with a focus on shelfbreak regions, including non-hydrostatic effects. Our research objectives are to:
- Apply our theory and schemes for rigorous optimal path planning and persistent ocean sampling with swarms of autonomous vehicles, and
- Further quantify the dynamics and variability of the circulation features and mixed layer, and the responses to monsoon winds, utilizing multi-resolution data-assimilative ocean modeling and process studies.
Objectives:
- Further develop, illustrate and determine the capabilities of the GMM-DO filter for multiscale data assimilation.
- Develop and utilize test cases and simulation experiments for the evaluation of data assimilation schemes in multiscale dynamics conditions.
- Study the multiscale properties of probability density functions predicted by GMM-DO, including multiple scales in time and multiple scales in space.
- Based on these properties, develop multi-resolution measurement operators and possibly multi-resolution GMM-DO filters and smoothers.
- Strengthen collaborations, transferring our test cases for multiscale data assimilation and our approaches to NRL. Utilize and leverage the MIT Naval Officer education program.
Presentations and Meetings
| Top of page |
Background Information
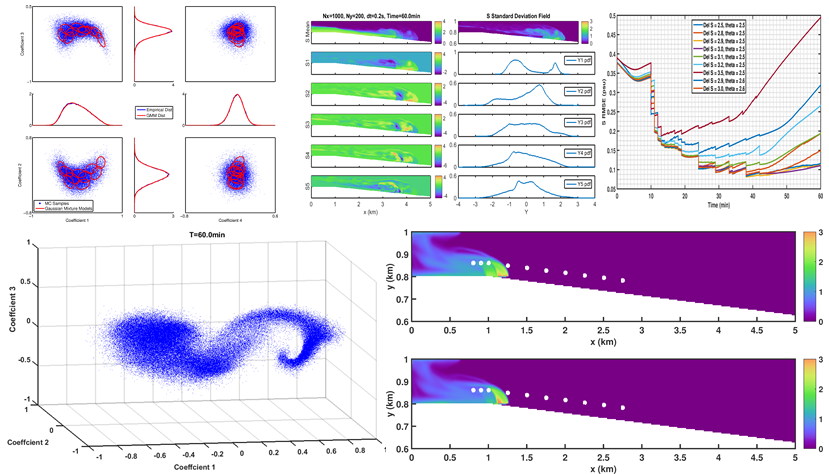
Nonlinear filtering and smoothing are open problems in many disciplines. This is the case in ocean modeling where state dimensions are O(10^6 - 10^9) and even a classic linear Kalman update is not directly feasible. To create an effective nonlinear filter, the MIT group combined its new Dynamically Orthogonal (DO) equations for uncertainty predictions with modern schemes in information theory and learning theory. A novel semi-parametric data assimilation framework was derived based on Gaussian Mixture Models (GMMs). In the resulting GMM-DO filter, the mixtures are fit to DO realizations, using an Expectation-Maximization algorithm and a Bayesian Information Criterion. Bayes' Law is then efficiently carried out analytically within the evolving DO subspace. We applied the GMM-DO filter to several time-dependent flows of dimensions O(10^5). We find that it strongly outperforms the Ensemble Kalman Filter and other methods, especially when the number of realizations is small compared to the size of the system and when observations are sparse or noisy. This is very promising since such attributes are common in ocean applications.
We are presently starting to implement our Dynamically Orthogonal (DO) equations into our MSEAS primitive-equation codes, specifically the structured hydrostatic PE code and the finiteelement non-hydrostatic solver. In the last year of this effort, it is possible that NRL will be interested in utilizing some of these schemes.
Our experience with multiscale data assimilation has been to assimilate data at the fastest scale modeled, regardless of the information content present in the observation. In other words, the observation is assimilated at the time it is sampled. However, as mentioned above, it is possible that multiscale connections or probability density functions in time and space would allow a better utilization of such observations. Either these pdf-based connections can be specified a priori or they can be predicted by a multiscale GMM-DO algorithm. Determining the issues and capabilities of these approaches are most relevant to this project.
We have also developed and implemented schemes and software to evaluate uncertainty predictions in the probabilistic sense, by comparisons to observed forecast errors and their probability densities, see http://mseas.mit.edu/Research/ONR6.2/. These schemes could be utilized in the present effort and transferred to NRL and other collaborators.
Specific Research Tasks
The coastal ocean is a prime example of multiscale dynamics. This is a consequence of turbulence, waves, tides, eddies, jets and currents, inflows from rivers, coastal winds inducing upwelling of cold, nutrient-rich waters, and rings and eddies from the deeper ocean drifting onshore, together with various remote influences. The shelfbreak is specifically a region of great interest, across a wide range of spatial and temporal scales. This is the focus of this proposal, in part because vertical velocities are often large there while the total depth is still limited, hence leading to potentially significant non-hydrostatic processes.
While traditionally grounded in linear theory and the Gaussian approximation, one recent research thrust for data assimilation has been the development of efficient assimilation methods that respect nonlinear dynamics and capture non-Gaussian features. Most such methods are either challenging to employ with large realistic systems or still based on heuristic hypotheses and ad hoc approximations. Our unique motivation here is to allow for realistic multiscale dynamics while rigorously utilizing the governing dynamical equations with information theory and learning theory for efficient Bayesian inference. To do so, we plan to employ the recent results of the MSEAS-group in such equation-based non-Gaussian data assimilation (Sondergaard and Lermusiaux, 2012a,b), combining the stochastic Dynamically Orthogonal (DO) field equations with semi-parametric Gaussian Mixture Models (GMMs). The challenge of our research will be to allow for truly multiscale inferences, where observations and models provide information on varied spatial and temporal scales.
Direct Multiscale Filtering and Smoothing
The multiscale data assimilation research will start with our new GMM-DO nonlinear filter. The filter is in theory directly capable of such nonlinear non-Gaussian multiscale data assimilation, without any modification. This holds at least for the Bayesian combination at a fixed time of forecast prior pdfs with observation likelihoods: all multiscale information at that time is in theory accounted for by a Bayesian update at the observation time. However, there remain several key research directions that can be investigated.
First, the theoretical GMM-DO capability will have to be evaluated in varied applications and simulation experiments (Sect. 2.2). This is because multi-scales and multi-physics models present data assimilation with several computational challenges. The main one is that observations then contain the multiscale and multi-physics information which need to be adequately distributed in time and space, and across physical components, by the assimilation scheme. For example, a measurement of ocean temperature in the coastal ocean contains a range of scales from smaller and faster scales due to turbulence, internal waves and tides to longer and slower scales due to seasonal variability and climate dynamics. How to ensure that this information is properly utilized at the right scales at the right time will need to be investigated and studied, both in idealized studies and in more realistic simulations.
Another research direction relates to the evolution and connections in time of these multiscale processes. Even though the Bayesian assimilation at a given fixed observation time accounts for all scales-connections at that time, the multiscale information still needs to be extracted and retained through time. A multi-time Bayesian update would allow the slower (and thus often larger) scales to be corrected over a longer time-period, while the faster (and often shorter) scales would be corrected over a shorter time-period. These times and space scales are possibly directly linked to the time and space scales of coherent structures (turbulence, waves, eddies, jets, etc.) and this can be investigated. In the fixed-time Bayesian update assimilation, it is the model dynamics which propagates the multiscale effect of the Bayesian assimilation at that fixed observation time. This would be strengthened by multi-time Bayesian updates, including Bayesian smoothing.
For the above investigations, we will first utilize and further implement our DO equations, GMM identification and overall GMM-DO filter in a multiscale modeling system. In the first two years, we will focus on idealized time-dependent 2D-in-space but multiscale dynamics (test cases are summarized in Section 2.2). In the second and third years, the results will then be utilized for the implementation (leveraging other funds) into more realistic simulation systems.
Other research directions include the study and visualization of the multiscale probability density function estimated by the GMM-DO filter. Multiscale error models using stochastic forcing and PDEs can also be developed, so as to represent model errors at multiple scales. Similarly, multiscale observation models and their pdfs can be determined.
If the present effort can be increased, we would also like to investigate multiscale smoothing using a GMM-DO smoother. Developing such a smoother would allow propagating the multiscale information contained in the observations both forward and backward in time.
Multi-Resolution Data Assimilation and Scale-Decomposition
A complementary approach to the above direct multiscale filtering and smoothing is based on arguments of scaledecomposition, and even scale separation if such separations can be justified. We have already utilized such multi-resolution approaches, both in optimal interpolation (e.g. Lermusiaux, 1999a; Haley et al, 2009; Haley and Lermusiaux, 2010) and in the initialization of ESSE ensembles (Lermusiaux et al, 2000; Lermusiaux, 2002). Notably, the latter ESSE initialization allows for correlations across scales.
The investigation of this multi-resolution approach will depend in part on the findings of the direct multiscale GMM-DO results. For example, we may find that the capabilities of direct GMM-DO filtering for multiscale data assimilation could be improved if scales are first decomposed, either in a correlated or in a non-correlated (separated) fashion. In fact, it is the study of the properties of the multiscale probability density function that we predict and estimate in the direct approach that will indicate if scale separation is possible or if a scale-decomposition could be useful. We note that this decomposition could include “correlations” in a non-Gaussian fashion, in some sense identified by the GMM representations. We will also study the timedependence of these GMM pdf-representations, investigating the non-Gaussian pdf relationships in time. The results of these pdf studies will indicate if a modification of the direct multiscale approach into a multi-resolution non-Guassian data assimilation scheme is useful.
In both the direct and the multi-resolution DA approaches, the observation operator or measurement model can also be defined as being multiscale or multi-resolution. To do so, the observations are decomposed into different scales or resolution prior to assimilation, and each scale or resolution has its own observation operator. As mentioned above for the scaledecomposition of the state, we note that these multi-resolution observation operators can be defined in an uncorrelated (separated), correlated, or non-Gaussian (e.g. GMM decomposed) fashion. For the first two definitions, our Fast Marching Method based Objective Analysis (FMM-based OA) codes (Agarwal and Lermusiaux, 2011) could be used to compute multiscale correlations and thus estimate these observation operators in applications with complex geometries.
Finally, we note that a possible drawback of the multi-resolution and scale-decomposition approach is the need to estimate these connections among observed variables either ahead of time or based on some approximate (scale-decomposed) models. If these decompositions are accurate, we suspect that the corresponding assimilation will work well. However, if they are not that accurate, if they should be dynamic but are maintained fixed, or if a scale-decomposition is not that appropriate, it is very likely that the PDE-based (original model) GMM-DO filter and smoother predictions of the pdf-connections will be more efficient. Our simulations studies (Sect. 2.2) should provide guidance to answer these questions.
Multiscale Adaptive Sampling and Modeling
Important feedbacks of data assimilation are adaptive sampling and adaptive modeling. Their research in the case of multiple scales and multiple dynamics is interesting but would require additional funding. This would involve both theoretical investigations and applications. Adaptive sampling is the acquisition of the most useful observations to optimally reduce uncertainties, while adaptive modeling is the machinelearning identification of the most useful model improvements (e.g. to optimally reduce model systematic errors/biases). Both of these activities involve computational fluid dynamics, control and optimization theory, information theory and machine learning. For multiscale dynamics, specific software would need to developed, possibly including cloud computing.
| Top of page |
References
-
Agarwal, A. and P.F.J. Lermusiaux, 2011. Statistical Field Estimation
for Complex Coastal Regions and Archipelagos. Ocean Modeling, 40(2), 164-189, doi:
10.1016/j.ocemod.2011.08.001.

-
Haley, P.J. Jr., P.F.J. Lermusiaux, A.R. Robinson, W.G. Leslie, O. Logutov, G. Cossarini, X.S. Liang, P. Moreno, S.R. Ramp, J.D. Doyle, J. Bellingham, F. Chavez, S. Johnston, 2009. Forecasting and Reanalysis in the Monterey Bay/California Current Region for the Autonomous Ocean Sampling Network-II Experiment. Special issue on AOSN-II, Deep Sea Research, Part II. ISSN 0967-0645, doi: 10.1016/j.dsr2.2008.08.010.

-
Haley, P.J., Jr. and P.F.J. Lermusiaux, 2010. Multiscale two-way embedding schemes for free-surface primitive-equations in the Multidisciplinary Simulation, Estimation and Assimilation System. Ocean Dynamics, 60, 1497-1537. doi:10.1007/s10236-010-0349-4.

-
Lermusiaux, P.F.J., 1999a. Data assimilation via Error Subspace Statistical Estimation. Part II: Middle Atlantic Bight shelfbreak front simulations and ESSE validation. Monthly Weather Review, 127(7), 1408-1432, doi: 10.1175/1520-0493(1999)127<1408:DAVESS>
2.0.CO;2.

-
Lermusiaux, P.F.J., D.G.M. Anderson and C.J. Lozano, 2000. On the mapping of multivariate geophysical fields: error and variability subspace estimates. The Quarterly Journal of the Royal Meteorological Society, April B, 1387-1430.

-
Lermusiaux, P.F.J., 2002. On the mapping of multivariate geophysical fields: sensitivity to size, scales and dynamics. Journal of Atmospheric and Oceanic Technology, 19, 1602-1637.

-
Sondergaard, T. and P.F.J. Lermusiaux, 2013b. Data Assimilation with Gaussian Mixture Models using the Dynamically Orthogonal Field Equations. Part II: Applications. Monthly Weather Review, 141, 6, 1761-1785, doi:10.1175/MWR-D-11-00296.1.

-
Sondergaard, T. and P.F.J. Lermusiaux, 2013a. Data Assimilation with Gaussian Mixture Models using the Dynamically Orthogonal
Field Equations. Part I. Theory and Scheme. Monthly Weather Review, 141, 6, 1737-1760, doi:10.1175/MWR-D-11-00295.1.

| Top of page |



