|
P.F.J. Lermusiaux, P.J. Haley, Jr., W.G. Leslie, T. Lolla, P. Lu, C. Mirabito, A. Phadnis, M. Ueckermann |
Massachusetts Institute of Technology
Mechanical Engineering Ocean Science and Engineering Cambridge, Massachusetts |
 |
ONR 6.2 Supported Publications |
ONR 6.1 Research |
Stochastic Forcing for Ocean Uncertainty Prediction
Our research vision is to develop and transform ocean modeling and data assimilation to quantify regional ocean dynamics on multiple scales. Our group creates and utilizes new models and methods for multiscale modeling, uncertainty quantification, data assimilation and the guidance of autonomous vehicles. We then apply these advances to better understand physical, acoustical and biological interactions. We seek both fundamental and applied contributions to build knowledge and benefit naval operations.
A main focus of this research is the role of stochastic forcing on ocean uncertainty and variability predictions. The work includes collaborations with NRL-Stennis to prepare the transfer of a subset of the capabilities and software developed by our Multidisciplinary Simulation, Estimation, and Assimilation Systems (MSEAS) group. This applied research in stochastic modeling and ocean uncertainty prediction is linked to two growing fundamental fields: prediction and reduction of uncertainties; and, estimation of properties by combining models with data. From a fundamental viewpoint, uncertainty is characterized by a probability density function (pdf). One of the aims of the applied research and collaborations with NRL will be to improve the prediction of such pdfs.
The research thrusts for this effort include:
- Stochastic forcing and uncertainty/variability predictions
- Sensitivity analysis for forecast quality control, data-model comparisons and data error models
- Multiscale covariance modeling and mapping
- Ensemble initialization and generation, towards non-Gaussian ensemble initialization
Our specific objectives are to:
- Develop, demonstrate and transfer techniques for stochastic error modeling and stochastic boundary forcing for improved ensemble uncertainty predictions with NCOM and COAMPS
- Develop and transfer software for ocean data management, quality control and automated robust distribution, including data error-models and data-model comparison codes
- Demonstrate and transfer techniques for multiscale covariance modeling and level-set-based objective analysis codes for mapping data in complex coastal/archipelago domains
- Develop and demonstrate ensemble initialization and generation schemes, towards non-Gaussian ensemble initialization
- Apply the above advances in collaborative sea exercises of opportunity
- Strengthen existing and initiate new collaborations with NRL, using and leveraging the MIT Naval Officer education program
Stochastic Forcing and Uncertainty/Variability Predictions
|
Discontinuous Galerkin Finite Element Methods:
We have extended our 3D-in-space Discontinuous Galerkin Finite Element (DGFE) Python Framework.
Within the Python framework, we had previously implemented simple meshing routines, 2D and 3D mesh
visualization using Mayavi, high-order advection schemes, and high-order Hybrid Discontinuous Galerkin
(HDG) diffusion schemes. Now we have implemented our novel HDG discretization for 2D or 3D ocean flows.
Our implementation works for hydrostatic or non-hydrostatic pressure and rigid-lid or free-surface flows.
For the free-surface version, we have mass-conserving schemes for both a fixed mesh approximation and a
moving mesh. The theoretical formulation of the novel HDG scheme has been improved by mathematically
finding the correct value of the HDG stabilization parameter for the pressure when using Projection
methods. Our HDG formulation has also been extended for vertical integration and implicit surface-pressure
calculation. Additionally, we have developed and implemented a new selective slope limiter to stabilize
the high-order computation, preventing Gibbs oscillations. We have validated the advection and diffusion
operators, verifying the correct rates of convergence, and we are currently validating the ocean model.
Work is underway on a parallel DGFE C/C++ framework, which is designed to optimize (and replace) several time-consuming routines used in the high-order HDG scheme. The implicit-explicit (IMEX) time stepping scheme has been re-implemented in C++ and in parallel using the PETSc library package, which in turn uses MPI for parallelism. Also, the Numpy C-API, along with improvements to the algorithms, has been used to speed up the mesh-building routines. Additionally, the mesh input procedure to the model has been modified and streamlined, and the model now accepts input generated by the meshing software GMSH and distmesh. As an example of results, we show the solution of the lock-exchange problem (Hartel et al., 2000) which tests the performance of solvers with a non-hydrostatic pressure under density-driven flows. Our solution is 2nd order accurate in time, 3rd order accurate in space, uses 66 elements in the vertical and 264 elements in the horizontal. Additionally, our new selective slope limiter is active in this simulation, and limits oscillations to less than 0.003 %. This result matches that of Hartel et al. (2000), a non-trivial result since our tests show that the shapes of the Kelvin-Helmholtz instabilities are sensitive to spatial resolution. We have also finished validating the advection and diffusion operators, and their spatial rates of convergence are plotted below. From the figures, we can see that we have nearly optimal convergence in all cases. We are currently validating the ocean solver, starting by validating the Navier-Stokes equations. |
|
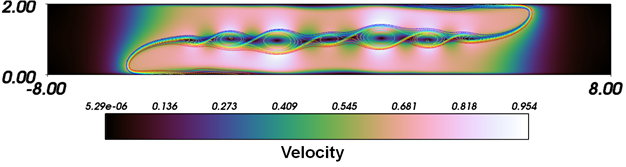 Density contours over velocity magnitude for the Lock Exchange problem with Gr = 1.25e6 at non-dimensional time T = 10. Our solution matches that of Hartel et al. (2000). This is a 3rd order accurate in space simulation using 66 elements in the vertical and 264 elements in the horizontal. |
|
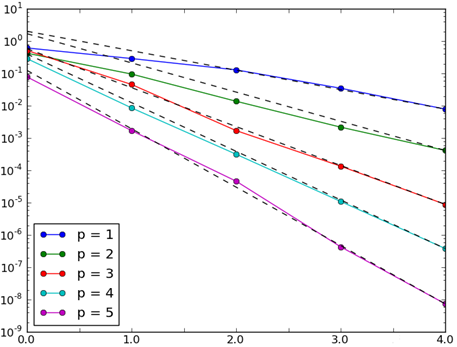 Convergence of advection operator for different orders of spatial approximation. Dashed lines give the theoretical convergence. |
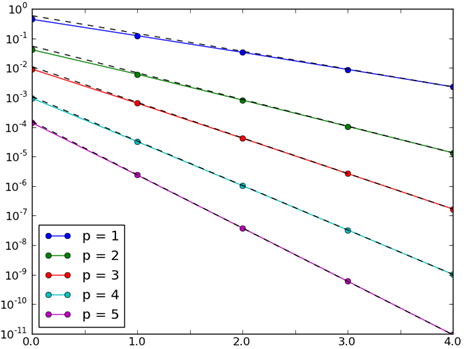 Convergence of diffusion operator for different orders of spatial approximation. Dashed lines give the theoretical convergence. |
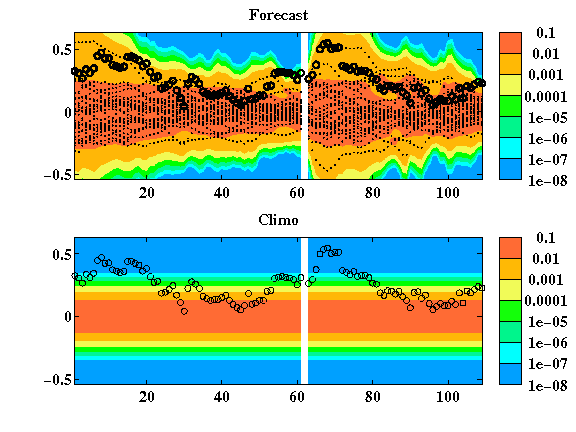
| Uncertain Boundary Conditions and DO Equations: Building on our DO equations, we derived and implemented a new efficient scheme for stochastic boundary conditions for Navier Stokes and Boussinesq equations. The scheme has now been validated using the 2D flow over a square cylinder in a confined channel. We have conducted a number of simulations spanning various Reynolds number ranges, and examined the behavior of the recirculation zone length, and vortex shedding period. We tested our scheme by varying the inlet velocity of the 2D flow over a square cylinder in a confined channel benchmark. The inlet velocity is varied by specifying a uniform probability density function on its magnitude. The range of Reynolds numbers is well resolved (equivalent to 105 Monte-Carlo simulations) and spans different dynamical regimes, e.g. from a steady flow with a recirculation zone to an unsteady flow with vortex shedding. Our DO solver is capable of correctly capturing the different flow regimes and their transitions. |
|
Uncertainty Quantification of Non-linear Dynamical Systems for Ocean Modeling:
A methodology and software have been developed for solving a generic system of stochastic differential equations.
The goal is to study multiple UQ methods and compare their capabilities and performance in handling uncertainties
pertaining to ocean modeling. The computations have been made efficient using sparsity of matrices. The software
has been used to study small and medium dimensional linear as well as non-linear systems with stochastic forcing
and uncertain initial and boundary conditions. The main novelty of the work is the focus on additive and
multiplicative noise, which is highly relevant to modeling of uncertainty in real ocean systems. The time
dependent polynomial chaos method has been further modified to handle stochastic forcing in full spatial
domain and its performance in comparison to the DO method has been analyzed.
Uncertainty in input parameters (including uncertain initial and boundary conditions) has been modeled using DO equations, generalized Polynomial Chaos and Monte Carlo methods. A modification of the polynomial chaos method to handle long time integration of non-linear systems with stochastic inputs has also been studied. We found that the modified time dependent polynomial chaos method is able to accurately model the evolution of uncertainty in input parameters but cannot handle stochastic forcing in large systems in its present form. We also found that since the time dependent polynomial chaos method in its present form is defined only in the full spatial domain, it is computationally more expensive than DO method, which can be implemented on a reduced time-dependent subspace. The DO method has been shown to be adequate for modeling both additive and multiplicative forcing and will be used to study uncertainty quantification in coupled ocean-acoustic systems. |
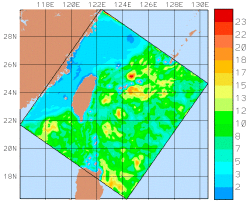
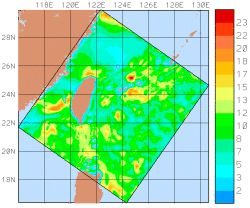
| Ocean Dynamics, Modeling and Assimilation: A barotropic velocity feature model was developed for the northern recirculation gyre of the Gulf Stream near the continental slope off the eastern US. Around Taiwan, a river discharge model was developed to account for the sudden large influx of freshwater from the island during and after the Typhoon Morakot, which occurred in August 2009. The model formulation and some results are described in Mirabito et al. (2012). |
Sensitivity analysis for forecast quality control, data-model comparisons and data error models
|
Data-model comparisons:
Data-model comparisons have been carried out for a number of projects in a variety of
regions (Philippines, Taiwan, Mid-Atlantic Bight, etc.) to examine model sensitivities, determine appropriate
initial and boundary conditions, resolve forcing uncertainties (especially atmospheric forcing), understand
implications of data coverage and availability, etc. Parameters for simulations were tuned to minimize
data-model differences. Appropriate combinations of atmospheric flux data, based on temporal and spatial
resolution and availability, from different models were determined for the QPE IOP09 and AWACS/SW06 experiments.
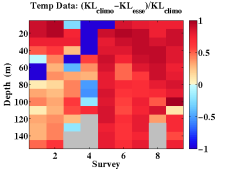
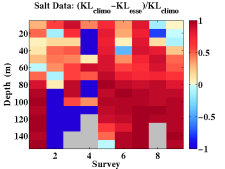
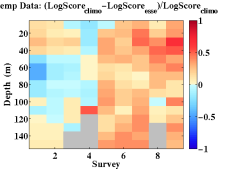
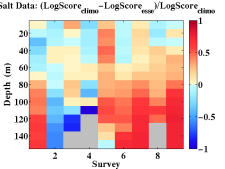
Data-model comparisons carried out for the QPE IOP09 experiment indicated that the climatological temperature and salinity data utilized for initial and boundary conditions were significantly different in structure and value from synoptic conditions. Typhoon Morakot generated a significant pulse of freshwater not represented by climatology and also modified typical local temperature structures. The climatological data was then modified as necessary to provide more accurate initial and boundary conditions. Data-model comparison also indicated where lack of real-time synoptic data proved critical in model evolution and provided an impetus to acquire additional synoptic data not available in real-time. Available atmospheric flux data sets for QPE IOP09 were carefully compared and evaluated: flux by flux and field by field. We subsequently selected what we determined was the most appropriate combination of re-analysis products and gridded those on 4 different grids at different resolutions. We then selected the highest resolution among all available fields and compiled/combined/merged them into our best estimates of the atmospheric forcing. A combination of 18km COAMPS and nested 15km/5km COAMPS data sets were chosen as the basis for the final product set which was distributed to all QPE PIs. For the AWACS/SW06 experiment, data-model comparisons led to: an increase in vertical discretization using 100 levels, with their distribution optimized to the thermocline structure ; the use of improved E-P and direct fluxes from WRF and NOGAPS in the atmospheric forcing; the correction of amplitudes in the diurnal tidal components; and, upgraded initial conditions incorporating synoptic data and pseudo profiles to bolster the front, WOA climatology corrected to match 2006 slope conditions, a revised shelfbreak T/S front feature model, a Gulf Stream T/S feature model (based on synoptic data) and transport feature models for the Gulf Stream, slope recirculation gyre and the shelfbreak front. Improvements to the reanalysis methodology directly led to improved fidelity of the simulations. |
| Data/software management: A number of MSEAS software packages have been prepared for distribution. The version control of the software is being carried out via SVN, which was chosen after an examination of a number of version-control packages. Documentation of the software is initially generated through Doxygen and is then manually augmented. Software for ocean data management, including multi-platform, multi-sensor data quality control and statistical analysis of real-time observations, is being finalized. A paper detailing this work (Leslie et al., 2012) is nearing completion. |
Multiscale covariance modeling and level-set-based objective analysis codes
|
The MSEAS Fast-Marching Method Objective Analysis (FMM-OA) has been upgraded by the inclusion of an option to
use second order discretizations in the FMM algorithm. This upgrade also included upgrades to the initialization
scheme for the FMM algorithm and restructuring of the code for efficiency. A companion code was released to
compute 3D streamfunction fields from the mapped temperature/salinity fields. This code employs an algorithm
to minimize inter-island transports in complex archipelagos. Additional new features incorporated into the
FMM-OA code, include options for separate data files for synoptic and climatology data, explicitly constructing
and saving the large scale analysis fields and the synoptic scale error fields, and making it easier for the
user to provide their own structured grid to the FMM-OA. A manuscript is being completed.
The MSEAS FMM-OA employs an upwind difference scheme to construct the shortest ocean distance between a data point and every grid point. These distances are then used in the correlation functions to map the data onto the grid. By comparing the fields constructed in the open ocean using the FMM-OA with fields constructed using a Euclidean distance OA, we find that using our new second order numeric code reduces the errors in the OA fields by a factor of 2-3. |
Non-Gaussian Data Assimilation
| Two manuscripts on Gaussian Mixture Models - Dynamically Orthogonal (GMM-DO) data assimilation (Sondergaard and Lermusiaux, 2012,a,b) have been accepted for publication. We first derived the efficient non-Gaussian data assimilation scheme, focusing on a time-dependent stochastic subspace that respects nonlinear dynamics and captures non-Gaussian statistics as it occurs. The properties and capabilities of the resulting GMM-DO filter were assessed and exemplified by applications to two dynamical systems: (1) the Double Well Diffusion and (2) Sudden Expansion flows; both of which admit far-from-Gaussian statistics. |
| Top of page |